Поток Куэтта - Couette flow
В динамика жидкостей, Поток Куэтта это поток вязкий жидкость в пространстве между двумя поверхностями, одна из которых движется по касательной относительно другой. Конфигурация часто имеет форму двух параллельных пластин или зазора между двумя концентрическими цилиндрами. Поток движется за счет силы вязкого сопротивления, действующей на жидкость, но дополнительно может быть мотивирован приложенным градиентом давления в направлении потока. Конфигурация Куэтта моделирует определенные практические проблемы, такие как потоки в мантии Земли и атмосфере,[1] течь в слегка нагруженном опорные подшипники, и часто используется в вискозиметрия и продемонстрировать приближения обратимость.[2] Этот тип течения назван в честь Морис Куэтт, профессор физики Французского университета Анже в конце 19 века.
Планарный поток Куэтта

Поток Куэтта часто используется на курсах физики и инженерии для иллюстрации управляемый сдвигом жидкое движение. Самая простая концептуальная конфигурация предполагает наличие двух бесконечных параллельных пластин, разделенных расстоянием. . Одна пластина, скажем верхняя, перемещается с постоянной скоростью. в собственном самолете. Без учета градиентов давления Уравнения Навье – Стокса упростить до
где - пространственная координата, нормальная к пластинам, а - распределение скорости. Это уравнение отражает предположение о том, что поток однонаправленный. То есть только одна из трех составляющих скорости нетривиально. Если y берет начало на нижней пластине, граничные условия таковы: и . Точное решение
может быть найден путем двукратного интегрирования и решения для констант с использованием граничных условий. Примечательным аспектом потока является то, что напряжение сдвига постоянна во всей области течения.[3] В частности, первая производная скорости , постоянно. (Это видно из прямолинейного профиля на рисунке.) Согласно Закон вязкости Ньютона (Ньютоновская жидкость), напряжение сдвига является продуктом этого выражения и (постоянной) жидкости вязкость.
Запуск потока Куэтта[4][5]

На самом деле решение Куэтта не может быть достигнуто мгновенно. Проблема запуска задается
при начальном условии
с граничными условиями (как поток Куэтта)
Задачу можно преобразовать в однородную, вычитая устойчивое решение и используя разделение переменных, решение дается формулой
- .
Так как , устойчивый раствор Куэтта восстанавливается. Во время , устойчивое решение Куэтта будет почти достигнуто, как показано на рисунке. Время, необходимое для достижения устойчивого раствора, зависит только от расстояния между пластинами. и кинематическая вязкость жидкости, но не от того, насколько быстро перемещается верхняя пластина .
Течение Куэтта с градиентом давления[6]
Более общая ситуация течения Куэтта возникает, когда постоянный градиент давления накладывается в направлении, параллельном пластинам. Эту проблему изучали Х. С. Роуэлл и У. Д. Финлейсон.[7][8] Уравнения Навье – Стокса в этом случае упрощаются до
где жидкий вязкость. Дважды интегрировав приведенное выше уравнение и применив граничные условия (такие же, как в случае течения Куэтта без градиента давления), получим следующее точное решение
Градиент давления может быть положительным (неблагоприятный градиент давления) или отрицательным (благоприятный градиент давления). Следует отметить, что в предельном случае неподвижных пластин () поток называется Плоский поток Пуазейля с асимметричным (относительно горизонтальной средней плоскости) параболическим профилем скорости.
Сжимаемая плоскость течения Куэтта

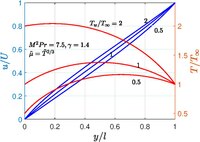
Эта проблема была впервые рассмотрена К.Р.Иллингвортом.[9] в 1950 г. В несжимаемом потоке профиль скорости линейный, потому что температура жидкости постоянна. Когда верхняя и нижняя стенки поддерживаются при разных температурах, профиль скорости усложняется, но оказывается, что он имеет точное неявное решение.
Рассмотрим плоское течение Куэтта[10] с нижней стенкой в состоянии покоя и свойствами жидкости, обозначенными нижним индексом и пусть верхняя стенка движется с постоянной скоростью со свойствами, обозначенными нижним индексом . Характеристики и давление на верхней стенке задаются и принимаются в качестве справочных величин. Позволять расстояние между двумя стенами. Граничные условия:
где это удельная энтальпия и это удельная теплоемкость. Сохранение массы и импульс показывает, что везде в области потока. Сохранение импульс и энергия уменьшаются до
где - напряжение сдвига стенки, но вся область течения принимает такое же напряжение сдвига, как и несжимаемое течение Куэтта. Расход не зависит от Число Рейнольдса , а скорее на Число Прандтля и число Маха , где это теплопроводность, это Скорость звука и это Коэффициент удельной теплоемкости. Оказывается, указанная проблема может быть решена неявно. Введем безразмерные переменные
Следовательно, решения
- тепло, передаваемое в единицу времени на единицу площади от нижней стены. Таким образом являются неявными функциями . Полезно записать решение в терминах температуры восстановления и энтальпия восстановления как температура изолированной стены, т. е. значение для которого . Тогда решение
Если удельная теплоемкость считается постоянной, то . Когда и , тогда и постоянны везде, таким образом восстанавливая несжимаемый раствор потока Куэтта. Кроме этого случая, нужно знать решить проблему. Когда и , величины восстановления становятся единицами . Есть ряд законов, которые нужно предсказать например, формула Сазерленда, степенной закон и т. д. Для воздуха значения обычно используются, и результаты для этого случая показаны на рисунке.
Липманн[11][12] изучили эффекты диссоциации и ионизации (т.е. не постоянна) и показал, что температура восстановления снижается за счет диссоциации молекул, а также изучил гидромагнетизм[13] эффекты на этот сжимаемый поток Куэтта.
Течение Куэтта в прямоугольном канале

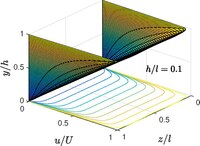
Одномерный поток действительно, когда обе пластины бесконечно длинные в продольном направлении и по размаху направление. Когда длина по размаху сделана конечной, поток становится двумерным. . Бесконечно большую длину в продольном направлении все еще необходимо удерживать, чтобы гарантировать однонаправленный характер течения.
Приведенная ниже проблема возникла у Роуэлла и Финлейсона (1928).[14] Рассмотрим бесконечно длинный прямоугольный канал с поперечной высотой и ширина по размаху , при условии, что верхняя стенка движется с постоянной скоростью . Без наложенного градиента давления Уравнения Навье – Стокса сократить до
с граничными условиями
С помощью разделение переменных, решение дается формулой
Когда классическая плоскость Куэтта восстанавливается, как показано на рисунке.
Течение Куэтта между коаксиальными цилиндрами
Течение Куэтта между коаксиальными цилиндрами[15] также известен как Поток Тейлора – Куэтта представляет собой поток, создаваемый между двумя вращающимися бесконечно длинными коаксиальными цилиндрами. Первоначальная проблема была решена Стокса в 1845 г.,[16] но Джеффри Ингрэм Тейлор имя было присвоено потоку, потому что он изучал устойчивость потока в своей знаменитой статье[17] в 1923 г. Если внутренний цилиндр с радиусом вращается с постоянной угловой скоростью и внешний цилиндр радиусом вращается с постоянной угловой скоростью , то скорость в направление дается
(Обратите внимание, что р заменил у в этом результате для отражения цилиндрических, а не прямоугольных координат). Из этого уравнения ясно, что эффекты кривизны больше не учитывают постоянный сдвиг в области потока, как показано выше.
Течение Куэтта между соосными цилиндрами конечной длины
В классической задаче течения Тейлора – Куэтта предполагаются цилиндры бесконечно большой длины, но эффекты конечной длины, которые встречаются в реальной жизни, более выражены в цилиндрической геометрии. Поток по-прежнему однонаправленный, и решение для с длиной цилиндра с помощью разделение переменных или используя интегральные преобразования дан кем-то[18]
где находятся Модифицированная функция Бесселя первого рода и Модифицированная функция Бесселя второго рода соответственно.
Смотрите также
- Поток Стокса-Куэтта
- Уравнение Хагена – Пуазейля
- Поток Тейлора – Куэтта
- Течение Хагена – Пуазейля из уравнений Навье – Стокса
использованная литература
- ^ Жиленко Д., Кривоносова О., Грицевич М., Рид П. (2018) Выбор волнового числа при наличии шума: результаты экспериментов. Хаос: междисциплинарный журнал нелинейной науки 28, 053110 https://doi.org/10.1063/1.5011349
- ^ Дж. П. Хеллер (1960) "Демонстрация без перемешивания" Американский журнал физики 28, 348-353.
- ^ Кунду П. и Коэн И. Механика жидкости.
- ^ Бэтчелор, Джордж Кейт. Введение в гидродинамику. Издательство Кембриджского университета, 2000.
- ^ Ачесон, Дэвид Дж. Элементарная гидродинамика. Издательство Оксфордского университета, 1990.
- ^ Джордж Кейт Бэтчелор,. Введение в гидродинамику. Издательство Кембриджского университета, 2000.
- ^ Роуэлл, Х.С. (1928). У. Д. Финлейсон. Инженерное дело 17, 606 (1922), 23, 249.
- ^ Бейтман, Х. (1932). Уравнения с частными производными математической физики. Уравнения в частных производных математической физики, Х. Бейтман, Кембридж, Великобритания: Cambridge University Press, 1932. С. 175.
- ^ Иллингворт, К. Р. «Некоторые решения уравнений течения вязкой сжимаемой жидкости». Математические труды Кембриджского философского общества. Vol. 46. № 03. Издательство Кембриджского университета, 1950.
- ^ Пако Лагерстрем. Теория ламинарного течения. Издательство Принстонского университета, 1996.
- ^ Липманн, Ханс Вольфганг, и Анатолий Рошко. Элементы газодинамики. Курьерская корпорация, 1957 год.
- ^ Liepmann, H. W., and Z. O. Bleviss. «Влияние диссоциации и ионизации на сжимаемый поток Куэтта». Douglas Aircraft Co., репт. СМ-19831 130 (1956).
- ^ Липманн, Х. В. "Гидромагнитные эффекты в потоке Куэтта и Стокса". Плазма в магнитном поле: симпозиум. Stanford University Press, 1958.
- ^ Роуэлл, Х.С. «У. Д. Финлейсон». Инженерное дело 17, 606 (1922) 23 (1928): 249.
- ^ Лев Ландау и Э. М. Лифшиц. «Гидромеханика Пергамона». Нью-Йорк 61 (1959).
- ^ Г. Г. Стоукс (1845) `` О теориях внутреннего трения движущихся жидкостей, а также о равновесии и движении упругих тел. in Mathematical and Physical Papers, стр. 102-104, Кембридж, Великобритания: Cambridge University Press, 1880.
- ^ Г. И. Тейлор (1923) "Устойчивость вязкой жидкости, содержащейся между двумя вращающимися цилиндрами", Философские труды Лондонского королевского общества. Серия А 223, 289–343.
- ^ Вендл, Майкл С. «Общее решение для профиля потока Куэтта». Физический обзор E 60.5 (1999): 6192.
- Ричард Фейнман (1964) Лекции Фейнмана по физике: главным образом электромагнетизм и материя, § 41–6 «Поток Куэтта», Аддисон – Уэсли ISBN 0-201-02117-X .














![{ displaystyle u (y, t) = U { frac {y} {h}} - { frac {2U} { pi}} sum _ {n = 1} ^ { infty} { frac { 1} {n}} e ^ {- n ^ {2} pi ^ {2} nu t / h ^ {2}} sin left [n pi left (1 - { frac {y}) {h}} right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/459f9ef09c94475acc580d6c1a45b9c625761b92)

























![{ displaystyle { tilde {h}} = { tilde {h}} _ {w} + left [{ frac { gamma -1} {2}} M ^ {2} Pr + (1 - { тильда {h}} _ {w}) right] { tilde {u}} - { frac { gamma -1} {2}} M ^ {2} Pr { tilde {u}} ^ {2 },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de93ae71157a0a626bb24e00d142113e8dd2c9a)

































