Симметрия двухатомных молекул - Symmetry of diatomic molecules
Молекулярная симметрия в физика и химия описывает симметрия присутствует в молекулы и классификация молекул по их симметрии. Молекулярная симметрия - фундаментальная концепция в применении Квантовая механика в физике и химии, например, его можно использовать для предсказания или объяснения многих свойств молекулы, таких как диполь момент и это позволено спектроскопические переходы (на основе правила отбора ) без выполнения точных строгих вычислений (что в некоторых случаях может быть даже невозможно). Для этого необходимо классифицировать состояния молекулы с помощью неприводимые представления от таблица символов группы симметрии молекулы. Среди всех молекулярных симметрий двухатомные молекулы обладают некоторыми отличительными особенностями, и их относительно легче анализировать.
Симметрия и теория групп
Физические законы, управляющие системой, обычно записываются в виде отношения (уравнения, дифференциальные уравнения, интегральные уравнения и т. Д.). Операция над ингредиентами этого отношения, которая сохраняет форму отношений неизменной, называется преобразованием симметрии или симметрией системы.
- Эти симметрия операции могут включать внешние или внутренние координаты; приводя к геометрической или внутренней симметрии.
- Эти операции симметрии могут быть глобальными или локальными; приводящие к глобальным или калибровочным симметриям.
- Эти операции симметрии могут быть дискретными или непрерывными.
Симметрия - принципиально важное понятие в квантовой механике. Он может предсказывать сохраняемые величины и предоставлять квантовые числа. Он может предсказать вырождение собственные состояния и дает представление о матричных элементах Гамильтониан без их расчета. Вместо того, чтобы смотреть на отдельные симметрии, иногда удобнее изучить общие отношения между симметриями. Оказывается, что Теория групп - наиболее эффективный способ сделать это.
Группы
Агруппа - математическая структура (обычно обозначается в виде (грамм, *)), состоящий из множестваграмм и бинарная операция (иногда свободно называемое «умножением»), удовлетворяющее следующим свойствам:
- закрытие: Для каждой пары элементов , тотовар .
- ассоциативность: Для каждогоИкс иу иz вграмм, обе (Икс*у)*z иИкс*(у*z) результат с тем же элементом вграмм (в символах, ).
- наличие личности: Должен быть элемент (скажем,е ) вграмм так что продукт любой элементграмм се не вносить изменений в элемент (в символах, ).
- наличие обратного: Для каждого элемента (Икс ) вграмм, должен быть элементу вграмм такой, что продуктИкс иу является элементом идентичностие (в символах, для каждого такой, что ).
- В дополнение к вышеперечисленным четырем, если так получится, что ,, т.е. операция в коммутативный, то группа называется Абелева группа. В противном случае это называется Неабелева группа.
Группы, симметрия и сохранение
Множество всех преобразований симметрии Гамильтониан имеет структуру группы, с групповым умножением, эквивалентным применению преобразований одно за другим. Элементы группы могут быть представлены в виде матриц, так что групповая операция становится обычным умножением матриц. В квантовой механике эволюция произвольной суперпозиции состояний задается унитарными операторами, поэтому каждый из элементов групп симметрии является унитарными операторами. Теперь любой унитарный оператор можно выразить как экспоненту некоторого Эрмитов оператор . Итак, соответствующие эрмитовы операторы - это 'генераторы ' из группа симметрии. Эти унитарные преобразования действуют на гамильтонов оператор в некоторых Гильбертово пространство таким образом, что гамильтониан остается инвариантным относительно преобразований. Другими словами, операторы симметрии коммутируют с гамильтонианом. Если представляет оператор унитарной симметрии и действует на гамильтониан , тогда;
Эти операторы обладают указанными выше свойствами группы:
- Операции симметрии замкнуты относительно умножения.
- Применение преобразований симметрии ассоциативно.
- Всегда существует тривиальное преобразование, при котором с исходными координатами ничего не делается. Это элемент идентичности группы.
- И пока существует обратное преобразование, оно является преобразованием симметрии, то есть оставляет гамильтониан инвариантным. Таким образом, инверсия является частью этого набора.
Итак, под симметрией системы мы понимаем набор операторов, каждый из которых ездит на работу с гамильтонианом, и они образуют группа симметрии. Эта группа может быть абелевой или неабелевой. В зависимости от того, какой из них, свойства системы меняются (например, если группа абелева, не будет вырождение ). В соответствии со всеми видами симметрии в системе, мы можем найти связанную с ней группу симметрии.
Отсюда следует, что генератор группы симметрии также коммутирует с гамильтонианом. Отсюда следует, что:
| Наблюдаемая, соответствующая образующей эрмитовой матрице, сохраняется. |
|---|
| Производная математического ожидания оператора T может быть записана как: Сейчас же, Так, поскольку H также является эрмитовым. Итак, у нас есть Сейчас же, как указано выше, и если оператор T не имеет явной зависимости от времени; константа, не зависящая от состояния может быть. Таким образом, наблюдаемая, соответствующая оператору T, сохраняется. |
Некоторыми конкретными примерами могут быть системы, имеющие вращающийся, трансляционная инвариантность и т.д. Для вращательно-инвариантной системы группа симметрии гамильтониана является общей группой вращений. Теперь, если (скажем) система инвариантна относительно любого вращения вокруг оси Z (т. Е. Система имеет осевая симметрия ), то группа симметрии гамильтониана - это группа вращения вокруг оси симметрии. Теперь эта группа порождается Z-компонентой орбитального углового момента: (элемент общей группы ). Таким образом, ездит с для этой системы и Z-компонента углового момента сохраняется. Точно так же трансляционная симметрия приводит к сохранению количества движения, инверсионная симметрия приводит к сохранению четности и так далее.
Геометрические симметрии
Операции симметрии, точечные группы и группы перестановки-обращения
Молекула, находящаяся в равновесии в определенном электронном состоянии, обычно имеет геометрическую симметрию. Эта симметрия описывается некоторым точечная группа который состоит из операций (называемых операциями симметрии), которые производят пространственную ориентацию молекулы, неотличимую от исходной конфигурации. Существует пять типов операции симметрии точечной группы: тождество, вращение, отражение, инверсия и неправильное вращение или вращение-отражение. Общим для всех операций симметрии является то, что геометрическая центральная точка молекулы не меняет своего положения; отсюда и название точечная группа. Можно определить элементы точечной группы для конкретной молекулы, учитывая геометрическую симметрию ее молекулярной модели. Однако, когда используется точечная группа, элементы не следует интерпретировать одинаково. Вместо этого элементы вращаются и / или отражают вибронные (колебательно-электронные) координаты, и эти элементы коммутируют с вибронным гамильтонианом. Точечная группа используется для классификации вибронных собственных состояний по симметрии. Классификация симметрии вращательных уровней, собственных состояний полного (ровибронного ядерного спина) гамильтониана, требует использования соответствующей группы перестановки-инверсии, введенной Лонге-Хиггинс.[1] См. Раздел Симметрия инверсии и симметрия ядерной перестановки ниже и Связь . Элементы групп перестановки-обращения коммутируют с полным молекулярным гамильтонианом. Помимо точечных групп, существует еще один вид групп, важных для кристаллография, где также необходимо позаботиться о переводе в 3-D. Они известны как космические группы.
Основные операции симметрии точечной группы
Вышеупомянутые пять основных операций симметрии:[2]
- Идентификационная операция E (от немецкого Einheit, что означает единство):Операция идентичности оставляет молекулу без изменений. Он образует элемент идентичности в группе симметрии. Хотя его включение кажется тривиальным, это важно еще и потому, что эта симметрия присутствует даже в самой асимметричной молекуле. Соответствующим элементом симметрии является сама молекула.
- Инверсия, я : Эта операция переворачивает молекулу вокруг ее центра инверсии (если он есть). Центр инверсии в этом случае является элементом симметрии. В этом центре может быть или не быть атома. Молекула может иметь центр инверсии, а может и не иметь. Например: молекула бензола, куб и сферы имеют центр инверсии, тогда как тетраэдр - нет.
- Отражение σ: Операция отражения создает зеркальное отображение молекулы в определенной плоскости. Плоскость зеркала делит молекулу пополам и должна включать ее геометрический центр. В этом случае плоскость симметрии является элементом симметрии. Плоскость симметрии, параллельная главной оси (определенная ниже), называется вертикальной (σv) и один перпендикулярный ему горизонтальный (σчас). Существует третий тип плоскости симметрии: если вертикальная плоскость симметрии дополнительно делит пополам угол между двумя осями двукратного вращения, перпендикулярными главной оси, плоскость называется двугранной (σd).
- п-Сложное вращение: Операция n-кратного вращения вокруг n-кратной оси симметрии создает ориентацию молекул, неотличимую от начальной для каждого вращения (по часовой стрелке и против часовой стрелки). Обозначается . Ось симметрии в этом случае является элементом симметрии. Молекула может иметь более одной оси симметрии; тот, у кого самый высокийп называетсяглавная ось, и по соглашению ось z назначается в декартовой системе координат.
- п-Вращение сгиба-Отражение или неправильное вращение Sп : Операция n-кратного неправильного вращения вокруг n-кратной оси неправильного вращения состоит из двух последовательных преобразований геометрии: во-первых, поворот через вокруг оси этого вращения, и, во-вторых, отражение через плоскость, перпендикулярную (и через молекулярный центр геометрии) к этой оси. Эта ось в данном случае является элементом симметрии. Это сокращенно Sп.
Все остальные симметрии, присутствующие в конкретной молекуле, представляют собой комбинацию этих 5 операций.
Обозначение Шенфлиса
ВSchoenflies (или жеSchönflies) обозначение, названный в честь немецкого математикаАртур Мориц Шенфлис, это одно из двух соглашений, обычно используемых для описания точечных групп. Это обозначение используется в спектроскопии и используется здесь для определения молекулярной точечной группы.
Точечные группы для двухатомных молекул
Для двухатомных молекул существуют две точечные группы: для гетероядерной диатомии и для гомоядерной диатомии.
- :
Группа , содержит вращения под любым углом вокруг оси симметрии и бесконечное количество отражений через плоскости, содержащие межъядерную ось (или вертикальную ось, что является причиной нижнего индекса 'v').В группе все плоскости симметрии эквивалентны, так что все отражения образуют единый класс с непрерывным рядом элементов; ось симметрии двусторонняя, так что существует непрерывный ряд классов, каждый из которых содержит два элемента . Обратите внимание, что эта группа Неабелева и в группе существует бесконечное число неприводимых представлений. Таблица символов группы выглядит следующим образом:
E | 2c∞ | ... | линейные функции, вращения | квадратичный | ||
|---|---|---|---|---|---|---|
| А1= Σ+ | 1 | 1 | ... | 1 | z | Икс2+ y2, z2 |
| А2= Σ− | 1 | 1 | ... | -1 | рz | |
| E1= Π | 2 | ... | 0 | (х, у) (RИкс, Ру) | (xz, yz) | |
| E2= Δ | 2 | ... | 0 | (Икс2-у2, ху) | ||
| E3= Φ | 2 | .... | 0 | |||
| ... | ... | ... | ... |
- :
Помимо симметрии осевого отражения, гомоядерные двухатомные молекулы симметричны относительно инверсии или отражения через любую ось в плоскости, проходящей через точку симметрии и перпендикулярной межъядерной оси.

Уроки группы можно получить из группы используя отношения между двумя группами: . Нравиться , является неабелева и в группе бесконечное число неприводимых представлений. Таблица символов этой группы выглядит следующим образом:
E | 2c∞ | ... | я | 2S∞ | ... | линейные функции, вращения | квадратичный | |||
|---|---|---|---|---|---|---|---|---|---|---|
| А1 г= Σ+грамм | 1 | 1 | ... | 1 | 1 | 1 | ... | z | Икс2+ y2, z2 | |
| А2 г= Σ−грамм | 1 | 1 | ... | -1 | 1 | 1 | ... | рz | ||
| E1 г= Πграмм | 2 | ... | 0 | 2 | ... | (х, у) (RИкс, Ру) | (xz, yz) | |||
| E2 г= Δграмм | 2 | ... | 0 | 2 | ... | (Икс2-у2, ху) | ||||
| E3g= Φграмм | 2 | .... | 0 | 2 | ... | |||||
| ... | ... | ... | ... | ... | ... | ... | ... | |||
| А1U= Σ+ты | 1 | 1 | ... | 1 | -1 | -1 | ... | z | ||
| А2u= Σ−ты | 1 | 1 | ... | -1 | -1 | -1 | ... | |||
| E1U= Πты | 2 | ... | 0 | -2 | ... | (х, у) | ||||
| E2u= Δты | 2 | ... | 0 | -2 | ... | |||||
| E3u= Φты | 2 | ... | 0 | -2 | ... | |||||
| ... | ... | ... | ... | ... | ... | ... | ... |
Сводные примеры
Группа точек | Симметрийные операции или групповые операции | Элементы симметрии или группировать элементы | Простое описание типовой геометрии | Групповой заказ | Кол-во классов и несводимый представительства (реставрации) | Пример |
|---|---|---|---|---|---|---|
| E, , σv | E, , | линейный |  Фтористый водород | |||
| E, , σчас ,я, | S∞ , E, ,, | линейный с центром инверсии |  кислород |
Полный набор коммутирующих операторов
В отличие от одиночного атома, гамильтониан двухатомной молекулы не коммутирует с . Итак, квантовое число больше не хорошее квантовое число. Межъядерная ось выбирает определенное направление в пространстве, и потенциал больше не является сферически симметричным. Вместо, и коммутирует с гамильтонианом (принимая произвольную межъядерную ось за Z ось). Но не ездить с из-за того, что электронный гамильтониан двухатомной молекулы инвариантен относительно поворотов вокруг межъядерной линии ( Z оси), но не при вращениях вокруг Икс или же Y топоры. Опять таки, и действуют в другом гильбертовом пространстве, поэтому они коммутируют с в этом случае тоже. Электронный гамильтониан двухатомной молекулы также инвариантен относительно отражений во всех плоскостях, содержащих межъядерную линию. (X-Z) плоскость является такой плоскостью, и отражение координат электронов в этой плоскости соответствует операции . Если - оператор, выполняющий это отражение, то . Итак Полный набор коммутирующих операторов (CSCO) для генерала гетероядерная двухатомная молекула является ; куда - оператор, инвертирующий только одну из двух пространственных координат (х или у).
В частном случае гомоядерной двухатомной молекулы существует дополнительная симметрия, поскольку в дополнение к оси симметрии, обеспечиваемой межъядерной осью, существует центр симметрии в средней точке расстояния между двумя ядрами (симметрия, обсуждаемая в этот абзац зависит только от того, что два ядерных заряда одинаковы. Следовательно, два ядра могут иметь разную массу, то есть они могут быть двумя изотопами одного и того же вида, такими как протон и дейтрон, или и , и так далее). Выбрав эту точку в качестве начала координат, гамильтониан будет инвариантным относительно обращения координат всех электронов относительно этого начала координат, а именно в операции . Таким образом, оператор четности . Таким образом, CSCO для гомоядерной двухатомной молекулы равен .
Символ молекулярного члена, Λ-удвоение
Символ молекулярного термина является сокращенным выражением представления группы и угловых моментов, которые характеризуют состояние молекулы. Это эквиваленттермин символ для атомного случая. Мы уже знаем CSCO самой общей двухатомной молекулы. Итак хорошие квантовые числа может в достаточной степени описать состояние двухатомной молекулы. Здесь симметрия явно указана в номенклатуре.
Угловой момент
Здесь система не является сферически симметричной. Так, , и государство не может быть изображено в терминах как собственное состояние гамильтониана не является собственным состоянием больше (в отличие от атомарного символа термина, где состояния были записаны как ). Но, как , собственные значения, соответствующие все еще можно использовать. Если,
куда - абсолютное значение (в а.е.) проекции полного электронного углового момента на межъядерную ось; может использоваться как символ термина. По аналогии со спектроскопическими обозначениями S, P, D, F, ..., используемыми для атомов, кодовые буквы принято связывать со значениями по переписке:

Для отдельных электронов используются следующие обозначения и соответствие:
и

Осевая симметрия
Опять таки, , и дополнительно: [в качестве ]. Отсюда сразу следует, что если действие оператора на собственном состоянии, соответствующем собственному значению из переводит это состояние в другое, соответствующее собственному значению , и что оба собственных состояния имеют одинаковую энергию. Электронные условия такие, что (то есть условия ), таким образом, двукратно вырождены, причем каждое значение энергии соответствует двум состояниям, различающимся направлением проекции орбитального углового момента вдоль оси молекулы. Это двукратное вырождение на самом деле является только приближенным, и можно показать, что взаимодействие между электронным и вращательным движениями приводит к расщеплению членов с на два соседних уровня, что называется -двоение.[3]
соответствует состояния. Эти состояния невырождены, так что состояния член может быть умножен только на константу при отражении через плоскость, содержащую ось молекулы. Когда , одновременные собственные функции , и могут быть построены. С собственные функции иметь собственные значения . Итак, чтобы полностью указать состояния двухатомных молекул, состояний, которые остаются неизменными при отражении в плоскости, содержащей ядра, необходимо отличать от состояния, для которых он меняет знак при выполнении этой операции.
Симметрия инверсии и симметрия ядерной перестановки
Гомоядерные двухатомные молекулы имеют центр симметрии в средней точке. Выбирая эту точку (которая является центром масс ядра) в качестве начала координат, электронный гамильтониан будет инвариантен относительно операции точечной группы я инверсии координат всех электронов в этом начале. Эта операция не является паритет операция P (или E *); операция четности включает в себя обращение ядерных и электронных пространственных координат в молекулярном центре масс. Электронные состояния либо остаются неизменными в процессе эксплуатации. я, или их знак меняется на я. Первые обозначены индексом грамм и называются герад а последние обозначены индексом ты и называются убрать. Индексы грамм или же ты поэтому добавляются к термину символ, так что для гомоядерных двухатомных молекул электронные состояния могут иметь симметрию , ...... согласно неприводимым представлениям точечная группа.
Полный гамильтониан двухатомной молекулы (как и всех молекул) коммутирует с паритет операционные P или E * и ровибронные (вращательно-колебательные-электронные) уровни энергии (часто называемые вращательными уровнями) могут быть обозначены меткой симметрии четности + или же -. Полный гамильтониан гомоядерной двухатомной молекулы также коммутирует с операцией перестановки (или обмена) координат двух (идентичных) ядер, а вращательные уровни получают дополнительную метку s или же а в зависимости от того, является ли полная волновая функция неизменной (симметричной) или измененной по знаку (антисимметричной) операцией перестановки. Таким образом, вращательные уровни гетероядерных двухатомных молекул маркируются + или же -, а гомоядерные двухатомные молекулы помечены + s, + а, -s или же -а. Ровибронные ядерные спиновые состояния классифицируются с использованием соответствующей группы перестановки-инверсии.[4]
Полный гамильтониан гомоядерной двухатомной молекулы (как и всех центросимметричных молекул) не коммутирует с операцией обращения точечной группы я из-за эффекта ядерного сверхтонкого гамильтониана. Ядерный сверхтонкий гамильтониан может смешивать вращательные уровни грамм и ты вибронные состояния (называемые орто-параграф смешивание) и передать орто-параграф переходы[5][6]
Вращение и полный угловой момент
Если S обозначает равнодействующую отдельных электронных спинов, являются собственными значениями S и, как и в случае с атомами, каждый электронный член молекулы также характеризуется величиной S. Если пренебречь спин-орбитальной связью, возникает вырождение порядка связаны с каждым для данного . Как и в случае атомов, величина называется кратностью термина и записывается как (левый) верхний индекс, так что символ термина записывается как . Например, символ обозначает такой член, что и . Стоит отметить, что основное состояние (часто обозначается символом ) большинства двухатомных молекул такова, что и демонстрирует максимальную симметрию. Таким образом, в большинстве случаев это состояние (записывается как , возбужденные состояния записываются как спереди) для гетероядерной молекулы и состояние (записывается как ) для гомоядерной молекулы.
Спин-орбитальная связь снимает вырождение электронных состояний. Это потому, что z-компонент спина взаимодействует с z-компонента орбитального углового момента, генерирующая полный электронный угловой момент вдоль оси молекулы Jz. Это характеризуется квантовым числом , куда . Опять же, положительные и отрицательные значения вырождены, поэтому пары (ML, MS) и (-ML, −MS) вырождены. Эти пары сгруппированы вместе с квантовым числом , которая определяется как сумма пары значений (ML, MS) для которого ML положительный:
Символ молекулярного термина
Итак, общий символ молекулярного термина для самой общей двухатомной молекулы дается следующим образом:
куда
- S полное спиновое квантовое число
- - проекция орбитального углового момента на межъядерную ось
- - проекция полного углового момента на межъядерную ось
- ты/грамм это эффект операции группы точек я
- +/− - симметрия отражения вдоль произвольной плоскости, содержащей межъядерную ось
правило фон Неймана-Вигнера непересечения
Влияние симметрии на матричные элементы гамильтониана
Электронные термины или потенциальные кривые двухатомной молекулы зависят только от межъядерного расстояния , и важно исследовать поведение этих потенциальных кривых при изменении R. Представляет значительный интерес изучить пересечение кривых, представляющих различные члены.

Позволять и две разные электронные потенциальные кривые. Если они пересекаются в какой-то точке, то функции и рядом с этой точкой будут соседние значения. Чтобы решить, может ли такое пересечение произойти, удобно поставить задачу следующим образом. Предположим, на некотором межъядерном расстоянии ценности и близки, но отчетливы (как показано на рисунке). Затем следует проверить, действительно ли и можно заставить пересекаться путем модификации . Энергии и являются собственными значениями гамильтониана . Соответствующие ортонормированные собственные состояния электронов обозначим через и и предполагаются действительными. гамильтониан теперь принимает вид , куда - оператор малого возмущения (хотя это вырожденный случай, поэтому обычный метод возмущения не работает). параметр , можно сделать вывод, что для и быть равным в точке должны быть выполнены следующие два условия:
| и |
|---|
| В качестве начального нулевого приближения вместо и сами по себе, их линейные комбинации вида , можно принять за собственное состояние гамильтониана (куда и являются, в общем, сложными). Подставляя это выражение в возмущенное Шредингер уравнение: Расширение: Взять внутренний продукт с соответствующим бюстгальтером: ; и Сейчас же, и являются собственными состояниями гамильтониана соответствующие различным собственные значения и, как сам по себе эрмитский, они ортонормированный: Таким образом: ; и Поскольку оператор эрмитово, матричные элементы и реальны, а . Условие совместимости для этих уравнений (такое, что оба и не равны одновременно нулю): Это дает: Эта формула дает искомые собственные значения энергии в первом приближении. Если значения энергии двух членов становятся равными в точке (т.е. члены пересекаются), это означает, что два значения заданные по формуле, одинаковы. Чтобы это произошло, выражение под радикалом должно исчезнуть. Поскольку это сумма двух квадратов, оба одновременно равны нулю. Итак, он дает условия: и |
Однако в нашем распоряжении только один произвольный параметр вызывая возмущение . Следовательно
два условия, включающие более одного параметра, в общем случае не могут быть выполнены одновременно (исходное предположение, что и реальный, означает, что тоже реально). Итак, могут возникнуть два случая:
- Матричный элемент тождественно пропадает. Тогда можно независимо удовлетворить первое условие. Следовательно, пересечение возможно, если для определенного значения (т. е. для определенного значения ) выполняется первое уравнение. В качестве оператора возмущения (или же ) коммутирует с операторами симметрии молекулы, этот случай произойдет, если два электронных состояния и имеют разные симметрии точечной группы (например, если они соответствуют двум электронным термам, имеющим разные значения , разные электронные паритеты грамм и ты, разные кратности, или, например, два члена и ), поскольку можно показать, что для скалярной величины, оператор которой коммутирует с операторами углового момента и инверсии, только матричные элементы для переходов между состояниями с одним и тем же угловым моментом и четностью отличны от нуля, и доказательство остается в силе, по существу, в в таком же виде для общего случая произвольного оператора симметрии.
- Если электронное состояние и имеют ту же симметрию точечной группы, то может быть и будет отличаться от нуля. За исключением случайного пересечения, которое произошло бы, если бы по совпадению два уравнения были выполнены при одном и том же значении , вообще невозможно найти одно значение (т. е. одно значение ), для которого одновременно выполняются два условия.
Таким образом, в двухатомной молекуле могут пересекаться только члены разной симметрии, а пересечение членов такой же симметрии запрещено. Это, в общем, верно для любого случая в квантовой механике, где гамильтониан содержит некоторый параметр, а его собственные значения, следовательно, являются функциями этого параметра. Это общее правило известно как фон Нейман - Вигнер правило непересечения. [примечания 1]
Этот общий принцип симметрии имеет важные следствия - молекулярные спектры. метод валентной связи в случае двухатомных молекул три основных соответствия между атомный и молекулярные орбитали заботятся о:
- Молекулярные орбитали, имеющие заданное значение (составляющая орбитального углового момента вдоль межъядерной оси) должна соединяться с атомными орбиталями, имеющими такое же значение (то есть такое же значение ).
- Электронная четность волновой функции (грамм или же ты) необходимо сохранить как варьируется от к .
- Необходимо соблюдать правило фон Неймана-Вигнера непересечения, чтобы кривые энергии, соответствующие орбиталям, имеющим такую же симметрию, не пересекались при варьируется от к .
Таким образом, правило непересечения фон Неймана-Вигнера также служит отправной точкой для теории валентных связей.
Наблюдаемые последствия
Симметрия в двухатомных молекулах проявляется непосредственно через влияние на молекулярные спектры молекулы. Влияние симметрии на различные типы спектров в двухатомных молекулах:
Вращательный спектр
В приближении электрического диполя можно показать, что амплитуда перехода для испускания или поглощения излучения пропорциональна вибронному матричному элементу составляющей электрический диполь оператор вдоль молекулярной оси. Это постоянный электрический дипольный момент. В гомоядерных двухатомных молекулах постоянный электрический дипольный момент исчезает, и чистый спектр вращения отсутствует (но см. N.B. Гетероядерные двухатомные молекулы обладают постоянным электрическим дипольным моментом и демонстрируют спектры, соответствующие вращательным переходам без изменения вибронного состояния. За , правила выбора для вращательного перехода: . За , правила выбора становятся: Это связано с тем, что, хотя поглощенный или испускаемый фотон несет одну единицу углового момента, вращение ядра может измениться без изменения , если электронный угловой момент изменяет одинаковое и противоположное значение. Соображения симметрии требуют, чтобы электрический дипольный момент двухатомной молекулы был направлен вдоль межъядерной линии, и это приводит к дополнительному правилу отбора .Чистый вращательный спектр двухатомной молекулы состоит из линий в дальнем инфракрасном или микроволновом диапазоне, частоты этих линий определяются выражением:
; куда , и
- N.B. В исключительных случаях сверхтонкий гамильтониан может смешивать вращательные уровни грамм и ты вибронные состояния гомоядерных двухатомных молекул, приводящие к чисто вращательным (орто - параграф) переходы в гомоядерной двухатомной молекуле.[6]
Колебательный спектр
Матричные элементы перехода для чисто колебательного перехода: , куда - дипольный момент двухатомной молекулы в электронном состоянии . Поскольку дипольный момент зависит от длины связи , его изменение при смещении ядер из равновесия можно выразить как: ; куда - дипольный момент при нулевом смещении. Таким образом, элементами матрицы перехода являются: с использованием ортогональности состояний. Таким образом, матрица перехода отлична от нуля, только если дипольный момент молекулы изменяется со смещением, иначе производные от будет ноль. Тогда грубое правило отбора для колебательных переходов двухатомных молекул таково: Чтобы показать колебательный спектр, двухатомная молекула должна иметь дипольный момент, который изменяется с расширением. Так, гомоядерные двухатомные молекулы не испытывают электродипольных колебательных переходов. Итак, гомоядерная двухатомная молекула не показывает чисто колебательных спектров.
При малых смещениях можно ожидать, что электрический дипольный момент молекулы будет линейно изменяться с удлинением связи. Это будет иметь место в случае гетероядерной молекулы, в которой частичные заряды двух атомов не зависят от межъядерного расстояния. В таких случаях (известных как гармоническое приближение) квадратичные и более высокие члены в разложении можно игнорировать и . Теперь матричные элементы могут быть выражены в базисе положения через волновые функции гармонического осциллятора: полиномы Эрмита. Используя свойство полиномов Эрмита: , очевидно, что что пропорционально , производит два члена, один пропорциональный а другой . Итак, единственные ненулевые вклады в происходит от . Итак, правило отбора для гетероядерных двухатомных молекул:
- Вывод: Гомоядерные двухатомные молекулы не показывают чистых колебательных спектральных линий, а колебательные спектральные линии гетероядерных двухатомных молекул регулируются вышеупомянутым правилом отбора.
Колебательный спектр
Гомоядерные двухатомные молекулы не показывают ни чисто колебательных, ни чисто вращательных спектров. Однако, поскольку поглощение фотон требует, чтобы молекула занимала одну единицу угловой момент, колебательные переходы сопровождаются изменением вращательного состояния, которое подчиняется тем же правилам отбора, что и для чистого вращательного спектра. Для молекулы в состояние, переходы между двумя колебаниями-вращениями (или колебательный) уровни и , с колебательными квантовыми числами и , распадаются на два набора в зависимости от того, или же . Набор, соответствующий называется R ветвь. Соответствующие частоты даются как:
Набор, соответствующий называется P ветвь. Соответствующие частоты даются как:
Обе ветви составляют то, что называется вращательно-колебательная полоса или вращательно-колебательная полоса. Эти группы находятся в инфракрасный часть спектра.
Если молекула не находится в состояние, так что , переходы с разрешены. Это порождает новую ветвь колебательно-вращательного спектра, называемую Q ветвь. Частоты соответствующие прямым в этой ветви задаются квадратичной функцией если и неравны и сводятся к одной частоте: если .
Для гетероядерной двухатомной молекулы это правило отбора имеет два следствия:
- И колебательные, и вращательные квантовые числа должны измениться. Поэтому Q-ветвь запрещена.
- Изменение энергии вращения может быть либо вычтено, либо добавлено к изменению энергии вибрации, давая P- и R-ветви спектра соответственно.
Гомоядерные двухатомные молекулы также демонстрируют такие спектры. Однако правила отбора немного другие.
- Вывод: Как гомо-, так и гетеро-ядерные двухатомные молекулы демонстрируют колебательные спектры. Q-ветвь отсутствует в спектрах гетероядерных двухатомных молекул.
Особый пример: ион молекулы водорода.
Явное влияние симметрии на молекулярную структуру может быть показано в случае простейшей биядерной системы: ион молекулы водорода или катион дигидорода, . Естественная пробная волновая функция для определяется, сначала рассматривая самое низкоэнергетическое состояние системы, когда два протона широко разделены. Тогда есть два возможных состояния: электрон присоединен к одному из протонов, образуя атом водорода в основное состояние, или электрон присоединяется к другому протону, снова в основном состоянии атома водорода (как показано на рисунке).

В испытании указано в позиционной основе (или вволновые функции ') тогда:
и
Анализ использование вариационного метода начинает принимать эти формы. Опять же, это только одна возможная комбинация состояний. Могут быть и другие комбинации состояний, например, электрон находится в возбужденном состоянии атома водорода. Соответствующий гамильтониан системы:
Ясно, что используя состояния и в качестве базиса введем недиагональные элементы в гамильтониан. Здесь из-за относительной простоты ион, матричные элементы действительно можно рассчитать. Электронный гамильтониан коммутирует с операцией симметрии обращения точечной группы я. Используя его свойства симметрии, мы можем связать диагональ и недиагональные элементы гамильтониана как:
| Диагональные условия: Где, - энергия основного состояния атома водорода. Опять таки, где последний шаг следует из того, что и из-за симметрии системы значения интегралов одинаковы. Теперь недиагональные термины: вставив полный набор состояний в последний срок. называется интегралом перекрытия И, (поскольку волновые функции действительны) Так, |
Потому что а также , линейная комбинация и который диагонализует гамильтониан (после нормализации). Теперь как я за , Штаты также являются собственными состояниями я. Оказывается, что и являются собственными состояниями я с собственными значениями +1 и -1 (другими словами, волновые функции и являются gerade (симметричными) и ungerade (несимметричными) соответственно). Соответствующие математические ожидания энергий равны .
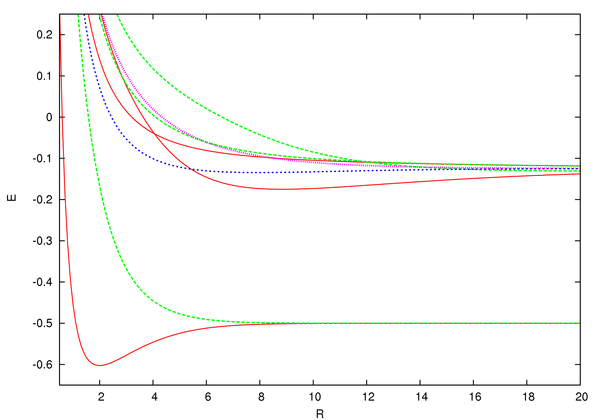
Из графика мы видим, что только имеет минимум, соответствующий разделению 1,3 Å, а полная энергия , что меньше начальной энергии системы, . Таким образом, только состояние Герада стабилизирует ион с энергия связи из . В результате основное состояние является и это состояние называется связывающей молекулярной орбиталью.[8]
Таким образом, симметрия играет явную роль в формировании .
Смотрите также
- Таблица символов
- Неприводимое представление § Приложения в теоретической физике и химии
- Четность (физика) § Молекулы
- Двухатомная молекула
- Молекулярная симметрия
- Обозначение Шенфлиса
- Список таблиц символов для химически важных групп трехмерных точек
- Дела Хунда
- Вращательно-колебательная спектроскопия
- Символ молекулярного термина
- Избегаемый переход
- Катион дигидрогена
- Симметрия в квантовой механике
- Группа (математика)
- Группы точек в трех измерениях
- Полный набор коммутирующих наблюдаемых
- Приближение Борна-Оппенгеймера
Примечания
- ^ Это следует из более общего правила теории групп. В терминологии теории групп общим условием возможного пересечения терминов является принадлежность терминов к разным неприводимые представления (арматуры) группы симметрии гамильтониана системы.[7]
Рекомендации
- ^ Лонге-Хиггинс, Х. (1963). «Группы симметрии нежестких молекул». Молекулярная физика. 6 (5): 445–460. Bibcode:1963молФ ... 6..445л. Дои:10.1080/00268976300100501.
- ^ http://csi.chemie.tu-darmstadt.de/ak/immel/script/redirect.cgi?filename=http://csi.chemie.tu-darmstadt.de/ak/immel/tutorials/symmetry/index1. html
- ^ B.H. Брансден, К.Дж. Иоахайн (24 апреля 2003 г.). Физика атомов и молекул (2-е издание). Прентис Холл. ISBN 978-8177582796.
- ^ П. Р. Банкер и П. Дженсен (2005), Основы молекулярной симметрии (CRC Press) ISBN 0-7503-0941-5 Раздел 8.3.4 [1]
- ^ Pique, J. P .; и другие. (1984). "Нарушение симметрии Унгерада-Герада, вызванное сверхтонкой структурой, в гомоядерной двухатомной молекуле вблизи предела диссоциации:я на − Предел ». Phys. Rev. Lett. 52 (4): 267–269. Bibcode:1984ПхРвЛ..52..267П. Дои:10.1103 / PhysRevLett.52.267.
- ^ а б Critchley, A. D. J .; и другие. (2001). "Прямое измерение перехода чистого вращения в H". Phys. Rev. Lett. 86 (9): 1725–1728. Bibcode:2001ПхРвЛ..86.1725С. Дои:10.1103 / PhysRevLett.86.1725.
- ^ Л. Д. Ландау и Л. М. Лифшиц (1 января 1981 г.). Квантовая механика, третье издание: нерелятивистская теория (том 3). Pergamon Press. ISBN 978-0750635394.
- ^ Таунсенд, Джон С. Современный подход к квантовой механике (2-е издание). Книги университетских наук. ISBN 978-1891389788.
дальнейшее чтение
- Квантовая механика, третье издание: нерелятивистская теория (том 3) Л. Д. Ландау, Л. М. Лифшица; ISBN 978-0750635394 Издание: 3-е; главы: XI и XII.
- Физика атомов и молекул Б.Х. Брансден, К.Дж. Иоахейн; ISBN 978-8177582796 Издание: 2-е издание; Глава 9
- Молекулярные спектры и молекулярная структура: спектры двухатомных молекул Герхарда Герцберга; ISBN 978-0894642685 Издание: 2-е
- Молекулярная квантовая механика Питера У. Аткинса, Рональда С. Фридмана; ISBN 978-0199541423 Издание: 5-е; глава: 10.
- Конспект лекций по квантовой механике (раздаточный материал: 12, 10 ) проф. Суренду Гупта, Институт фундаментальных исследований Тата, Мумбаи.
- Симметрия в физике: принципы и простые приложения Том 1 Джеймс Филип Эллиотт, П.Г. Даубер; ISBN 978-0195204551
- Джон С. Таунсенд «Современный подход к квантовой механике»; Издание 2-е; ISBN 978-1891389788
- http://www.astro.uwo.ca/~jlandstr/p467/lec5-mol_spect/index.html
внешняя ссылка
- http://www.astro.uwo.ca/~jlandstr/p467/lec5-mol_spect/index.html
- http://csi.chemie.tu-darmstadt.de/ak/immel/script/redirect.cgi?filename=http://csi.chemie.tu-darmstadt.de/ak/immel/tutorials/symmetry/index1. html
- http://theory.tifr.res.in/~sgupta/courses/qm2014/index.php
- PDF-файл, объясняющий связь между точечными группами и группами перестановки-инверсии. Связь













![[H, U] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb1374f210c431cfb9e40d879eabcc15a2ff64f2)
![{ begin {align} & {H} '= {{U} ^ {{ dagger}}} HU = H & Rightarrow HU = UH & Rightarrow [H, U] = 0; forall U in G конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59a25b775a12acb0dbe984613d06835ad81a79c5)




![{ frac {d left langle T right rangle} {dt}} = { frac {1} {i hbar}} left langle [H, T] right rangle + left langle { frac { partial T} { partial t}} right rangle](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dcaf66b99eea060ba0cee504b9f8b29d205d089)
![[H, T] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/18e4a4a719b44b9139dc6051312abcc76237932b)




































![[{{A} _ {{y}}}, H] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/914a87c7851fd0dfc0dfc59c4bd7bce1bd25df32)







![[H, {{L} ^ {{2}}}] neq 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca7e84c594b01b234c110e890de21af0d0d892ac)

![[H, {{L} _ {{z}}}] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/f49d96930f20c42c5665eb047c8130ca13316716)












































































































































![{ displaystyle] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c423490075b6646360ef8fd388c06d5c2859cff6)


















